ТОРА (9) - Лекция №6 - Алгоритм построения хорошей БД

Третья нормальная форма

Пример аномалий у 3НФ

$R = (A, B, C, D)$ и $F = (A\rightarrow B, B\rightarrow A, AC\rightarrow D)$

Два ключа:

первый - $AC$:

$(AC)^+=ACBD = R$

$A^+=AB\neq R$

$C^+ = C\neq R$

второй - $BC$:

$(BC)^+=BCAD = R$

$B^+ = BA\neq R$

Покажем, что в этом случае $R$ находится в 3НФ:

1)

неключевой атрибут $H$, $H = D$

2)

$Y\rightarrow H$, $H\notin Y$, $Y = AC$

3)

$X = BC$, $X = AC$

Нельзя подобрать нужную тройку, потому $R$ находится в 3НФ. Однако, отношение всё равно обладает аномалиями:

• избыточности: наименование поставщика повторяется для каждой поставляемой делали;
• противоречивости при изменении наименования поставщика надо изменить его во всех записях, куда оно входит;
• включения: нельзя включить информацию о поставщике, если он ничего не поставляет;
• удаления: при удалении детали удаляется информация о поставщике.

Для устранения этого вводится усиленная 3НФ - Бойса-Кодда.

Нормальная форма Бойса-Кодда

ФЗ $X\rightarrow Y$ является неприводимой, если для любого подмножества $Z\subset X$ выполняется $Z\nrightarrow Y$ или $Z\rightarrow Y\notin F^+$

Пусть есть отношение $R$ и $F$ включает в себя нетривиальные неприводимые ФЗ. Тогда отношение $R$ находится в нормальной форме Бойса-Кодда, если для любого $X\rightarrow Y\in F$ => $X$ - ключ.

Пример:

$R_1 = AB$, $F_1 = (A\rightarrow B, B\rightarrow A)$, $A$ - ключ, $B$ - ключ.

или

$R_2 = ACD$, $F_2 = (AC\rightarrow D)$, $AC$ - ключ.

Алгоритм синтеза "хорошей" БД

Пусть $U$ - универсальная схема отношения (множество всех атрибутов предметной области) и $F$ - множество ФЗ.

Перед выполнением алгоритма можно привести все ФЗ к одному атрибуту в правой части (по свойству декомпозиции) и удалить лишние ФЗ. Но это не обязательно.

Алгоритм:

1. построить УНП для $F$;
2. если среди ФЗ в УНП нет ФЗ, включающей все атрибуты из $U$, то добавить в УНП тривиальную ФЗ $U\rightarrow\varnothing$. Выполнение этого шага почти всегда обеспечивает свойство соединения без потерь будущей схемы БД;
3. привести все нетривиальные ФЗ из УНП к неприводимому виду (удалить лишние атрибуты в левых частях ФЗ);
4. разбить полученное множество ФЗ УНП на классы эквивалентности. Две зависимости $X_i\rightarrow Y_i$ и $X_j\rightarrow Y_j$ будем называть эквивалентными, если $X_iY_i = X_jY_j$. Далее введём обозначение $K_r = X_iY_i$ - множество атрибутов в левой и правой частях ФЗ $r$-того класса эквивалентности;
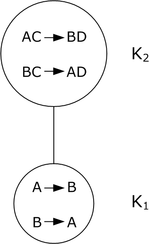
5. построить граф иерархии полученных на предыдущем шаге классов эквивалентности (если это возможно). Правило построения: $j$-ый узел соединяем снизу с $i$-ым узлом, если $K_j\subset K_i$. В каждом узле записываются все ФЗ, соответствующего класса эквивалентности;
6. из каждого класса эквивалентности в графе иерархии оставить только одну ФЗ. Правила выбора:
   1. удалить из класса эквивалентности лишние ФЗ;
   2. если в классе эквивалентности осталось больше одной ФЗ, то выбрать ФЗ с меньшим числом атрибутов в левой части;
   3. если у оставшихся ФЗ число атрибутов в левой части одинаково, то выбрать ту ФЗ, которая позволит редуцировать (вычеркнуть) атрибуты справа у ФЗ, расположенных выше в графе иерархии;
   4. если в результате не удалось выбрать ни одной, то выбрать произвольную;
7. редуцировать атрибуты справа в оставшихся ФЗ. Для этого просмотреть каждый путь снизу вверх в графе иерархии. Двигаясь по выбранному пути, выполнить следующие действия в каждом узле пути:
   1. пусть $X\rightarrow Y$ - это ФЗ, записанная в данном узле. Каждый атрибут, принадлежащий правой части, вычеркнуть в правых частях ФЗ, расположенных в узлах этого пути по иерархии выше;
   2. для тривиальной ФЗ $U\rightarrow\varnothing$ атрибуты вычёркиваются слева;
8. исключить из рассмотрения ФЗ с пустой правой частью (кроме редуцированной ФЗ $U\rightarrow\varnothing$). Исключённые на этом шаге ФЗ являются лишними и выводятся из оставшихся;
9. каждую оставшуюся в графе иерархий ФЗ $V\rightarrow W$ заменить на множество $VW$. Получившееся множество схем отношений обозначить как $\rho$;
10. для полученной на предыдущем шаге схемы БД проверить:
    1. обладает ли она свойством соединия без потерь. Если не обладает, то добавить ключ универсальной схемы $U$ в эту схему;
    2. обладает ли $\rho$ свойством сохранения ФЗ. Если нет, то, использовать зависимости, не вошедшие в проекцию $X\rightarrow Y\notin\Pi_{R_i}(F)$, для построения новых схем отношений, то есть добавить в $\rho$ $XY$.

После выполнения всех шагов полученная схема $\rho$:

• обладает свойством соединения без потерь;
• обладает свойством сохранения ФЗ;
• находится в 3НФ или НФБК;
• содержит минимальное число схем отношений.

Пример

$U = (поставщик, фирма, деталь, количество) = (A, B, C, D)$

$F = (A\rightarrow B, B\rightarrow A, AC\rightarrow D, BC\rightarrow D)$

Строим $\rho$:

1)

$УНП = (A\rightarrow B, B\rightarrow A, AC\rightarrow BD, BC\rightarrow AD)$

2)

пропускаем этот шаг, так как есть ФЗ (даже не одна), включающая все атрибуты из $U$

3)

уменьшить число атрибутов не удаётся

4)

1 класс: $A\rightarrow B$, $B\rightarrow A$, $K_1 = AB$

2 класс: $AC\rightarrow BD$, $BC\rightarrow AD$, $K_2 = ABCD$

5)

6)

для $K_2$:

способ 1 - как во втором семинаре

можно ли вывести $AC\rightarrow BD\in(BC\rightarrow AD)^+$?

$(AC)^+=AC$, $BD\nsubseteq(AC)^+$, значит нельзя

можно ли вывести $BC\rightarrow AD\in(AC\rightarrow BD)^+$?

$(BC)^+=BC$, $AD\nsubseteq(BC)^+$, значит нельзя

способ 2 - вычеркнуть из правых частей ФЗ рассматриваемых классов эквивалентностей общие атрибуты. Если получаются ФЗ с пустой правой частью, то они являются лишними.

$AC\rightarrow B$

$BC\rightarrow A$

выше по иерархии ничего нет, выбираем $BC\rightarrow AD$

нет лишних ФЗ, потому...

для $K_1$:

продолжение...